Процессы при резании на станках с ЧПУ

Расчет динамических процессов при резании и их влияние на точность обработки

Расчетная схема станка при резании охватывает замкнутую динамическую систему полностью. Однако для анализа удобно представить динамическую систему в виде эквивалентной одноконтурной системы (рис. 8.13). Эквивалентной упругой системой в этом случае является динамическая система станка при вспомогательных и установочных движениях.

Прямая связь в динамической системе при резании выражается силой резания, деформирующей эквивалентную упругую систему. Обратная связь реализуется через изменение толщины срезаемого слоя (при обработке с толщиной срезаемого слоя существенно меньшей, чем его ширина) при деформировании системы.

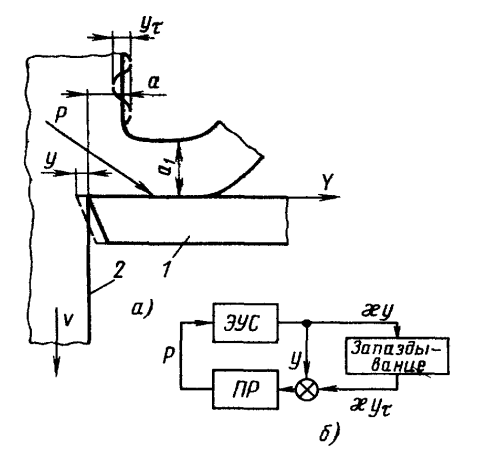
Рис. 8.13. Схема смещений y резца (1) и заготовки (2) при резании (а) и эквивалентная динамическая система станка при резании (б): у_х — изменение толщины срезаемого слоя, равное смещению резца и заготовки при предыдущем ра­бочем ходе; х — коэффициент перекрытия следа по ширине срезаемого слоя

Обратная связь складывается из двух составляющих: одна совпадает по времени с деформированием, другая проявляется с некоторым запаздыванием во времени. Вторую составляющую называют регенеративной связью. Сущность ее заключается в том, что при относительном смещении инструмента и обрабатываемой заготовки на поверхности заготовки (или инструмента, например шлифовального круга вследствие его изнашивания) остается след в форме переменного припуска. При повторном проходе этот припуск входит в зону резания как «зафиксированная» на поверхности заготовки деформация, происходившая во время предшествующего рабочего хода. Время между рабочими ходами определяет время запаздывания. Иногда говорят, что первая составляющая обратной связи проявляется при резании «по чистому», а обе составляющие — при резании «по следу».

В зависимости от отношения ширины повторно срезаемого слоя к ширине исходного судят о коэффициенте х перекрытия, который может изменяться от нуля (при резании по чистому) до единицы при полном перекрытии, например при врезном точении или шлифовании.

Характеристика эквивалентной упругой системы станка (по связи с резанием) определяется в простейшем случае, достаточно широко распространенном, отношением изменения деформации (перпендикулярно поверхности резания) к внешней силе, соответствующей силе резания. Это модельное представление удобно при экспериментальном определении характеристики. При проектных расчетах характеристики системы нет необходимости в замене сложной схемы сил резания одной силой.

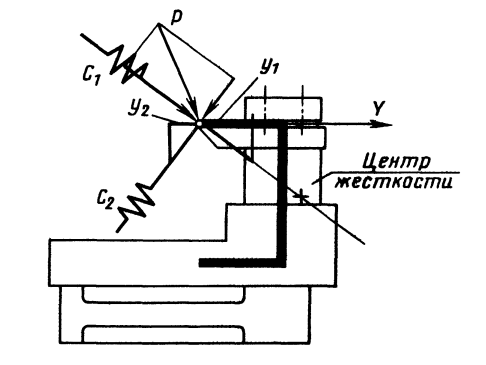
Рис. 8.14. Схема упрощенной модели эквивалент­ной упругой системы токарного станка

На рис. 8.14 показана схема упрощенной мо­дели ЭУС токарного станка при врезном попе­речном точении. Модель ЭУС принята плоской для простоты анализа. При этом обрабатывае­мая заготовка вращается, суппорт перемещает­ся. Перемещение вершины резца под действием силы резания определяется деформацией суп­порта как упругой системы» жесткость кото­рой в двух перпендикулярных направлениях различна. Ось максимальной жесткости направ­лена через центр жесткости суппорта.

Статическая характеристика (м/Н) эквива­лентной упругой системы К_эус=у/Р. Здесь у — изменение смещения вершины резца по оси Y, перпендикулярной к поверхности реза­ния; У=У₁—У₂, где У₁,У₂ — Проекции дефор­маций по осям жесткости на ось Y; Р — измене­ние силы, соответствующей силе резания.

В зависимости от знака смещения вершины резца (положительное смещение — от заготов­ки) возможны три случая: 1) у₁> у₂, у> 0; К_эус > 0; 2)у₁= у₂ , y=0; К_эус = 0; 3)у₁ < у₂, у< 0; К_эус < 0;

Наличие таких характеристик в сложных прост­ранственных упругих системах отмечалось в подразд. 8.3. Изложенное модельное пред­ставление необходимо для выявления принци­пиальных особенностей динамических процессов в станках. При проектном расчете эквивалент­ной упругой системы, имеющей более сложную расчетную схему, переход к такой модели не нужен.

Частотная характеристика системы в рассмат­риваемом случае является суммой частотных (комплексных) характеристик независимых (нормальных — по терминологии теории колеба­ний) колебательных систем с одной степенью свободы. На рис. 8.15 показан пример сложения характеристик этих систем, одна из которых имеет отрицательный статический коэффициент. Принципиально важной особенностью динамической частотной характеристики описанной модели упругой системы является охват ею всех квадрантов комплексной плоскости. Колебательная система с одной степенью свободы или цепная система с многими степенями свободы имеют частотные характеристики, лежащие в одной полуплоскости комплексной системы координат.

Экспериментально характеристики определяют, используя нагружающие устройства в виде вибраторов различных типов и измерительных преобразователей для фиксирования смещений между обрабатываемой заготовкой и инструментом. Изменяя частоту колебаний силы, создаваемой вибратором в рабочем диапазоне частот, определяют соотношение амплитуд и фазу смещения системы. Можно экспериментально определять частотные характеристики при других формах возмущающего воздействия, в частности при ударе. Полученные сигналы измерительных преобразователей силы и смещения подвергают математической обработке с помощью ЭВМ.

На практике определяют характеристики системы при резании на режимах, сопровождающихся появлением вибрации. Информация получается более полной, если используется безынерционный динамометр для фиксирования силы резания. В этом случае при математической обработке сигналов методами статистической динамики определяют отношение деформации ЭУС к силе резания. Преимущество этого метода — наиболее близкое соответствие получаемой информации реальным условиям работы станка. Однако практически при этом, как правило, оказывается ограниченным частотный диапазон получаемой характеристики.

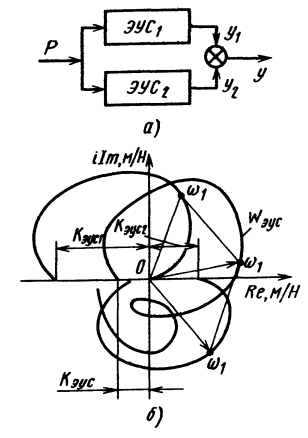
Рис. 8.15. Схема (а) и амплитудно-фазово-частот­ная характеристика (б) упрощенной модели эквива­лентной упругой системы по главным осям жестко­сти (по нормальным координатам)

Данные, получаемые при экспериментальном исследовании прототипа станка, используют при необходимости для уточнения параметров рас­четной схемы, а также при составлении рас­четных схем станков аналогичной конструкции.

В подвижном соединении инструмента и обра­батываемой заготовки реализуется рабочий процесс — резание. Основным параметром, оп­ределяющим связь деформации эквивалентной упругой системы с процессом резания, являет­ся изменение толщины срезаемого слоя. Резание как процесс упругопластического деформиро­вания содержит сложные внутренние связи между напряженным состоянием, деформаци­ями, тепловыми процессами и свойствами обра­батываемого материала. В зависимости от усло­вий резания (режима обработки, геометричес­ких параметров и материала режущего инстру­мента; материала заготовки и т. п.) резание мо­жет быть собственно устойчивым и неустойчи­вым. Устойчивому процессу соответствует об­разование сливной стружки, неустойчивому — стружки надлома, элементной, суставчатой, стружки со срывающимся наростом. В областях собственной неустойчивости резания возникает автоколебательный процесс стружкообразования. Примерное постоянство объемов формирующихся элементов стружки или срывающе­гося нароста определяет зависимость частоты автоколебательного процесса от скорости реза­ния: частота растет с увеличением скорости.

Статическая и динамическая характеристики резания могут быть определены только для собственно устойчивого стружкообразования, т е. при формировании сливной стружки. Ха­рактеристики выражают зависимость силы реза­ния от толщины срезаемого слоя.

Линеаризуя известные эмпирические зависи­мости, определяющие силу резания, можно пред­ставить статическую характеристику (Н/м) в следующем виде: К_Р = Р/у = Р_УДb. Здесь К_Р — статическая характеристика резания как эле­мента замкнутой динамической системы станка; Р — изменение (отклонение) силы резания; у — изменение (отклонение) толщины срезаемого слоя; Р_уд=σ₀ξ — удельная сила резания, Н/м², где σ₀ — некоторое условное напряжение типа временного сопротивления обрабатываемого ма­териала; ξ— усадка стружки, являющаяся ха­рактеристикой степени пластического деформи­рования материала; ξ=a₁/a (a₁—толщина стружки; а — толщина срезаемого слоя), Ь — ширина срезаемого слоя.

Динамическую характеристику резания оп­ределяют раздельно для сил на передней и на задней поверхностях резца (режущего элемен­та). Частотная характеристика резания для си­лы на передней поверхности режущего элемен­та W_рп(iω) =Р_рп(iω) /у(iω) =Kр/(iT_рω + 1), где Р_рп — изменение силы резания на передней поверхности; Т_р — постоянная времени резания (стружкообразования).

Величину Т_р (с) определяют расчетным путем или экспериментально, она характеризует отс­тавание изменения силы резания от изменения толщины срезаемого слоя: T_р = kɑ₀ξ₀/ʊ = l_Р/ʊ, где k= 1...1.5— коэффициент; ɑ₀ — заданная толщина срезаемого слоя; ξ₀ — заданное (уста­новившееся) значение усадки стружки, l_р — длина пути резания за время T_р , постоянная пути резания; ʊ — скорость резания.

Изменение силы на задней поверхности режущего элемента определяется значением контактной деформации резцом обработанной поверхности.

На рис. 8.16 показана схема формирова­ния контактной деформации при смещениях инструмента. При малых смещениях и постоян­ной высоте контактной площадки в первом при­ближении частотная характеристика резания по силе на задней поверхности имеет вид

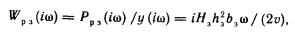
где Р_рз — изменение силы на задней поверх­ности резца; Н₃ — контактная жесткость (твер­дость материала обрабатываемой заготовки); h₃ — высота контактной площадки (фаска, площадка износа); Ь₃ — ширина контактной площадки (как правило, b₃> b за счет контакта вспомогательной поверхности).

Сила на задней поверхности пропорциональ­на первой производной координаты смещения или скорости колебаний. Изменение силы опе­режает во времени изменение толщины срезае­мого слоя при смещениях инструмента (но не изменения припуска). Указанная линейная за­висимость силы на задней поверхности резца от скорости колебаний (скорости врезания в за­готовку) является приближенной и использует­ся при условии А_у < (tgɑ/2) (ʊ/ω), где А_у — амплитуда колебаний в направлении, перпенди­кулярном к поверхности резания; a — задний угол резца.

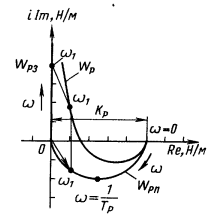
Рис. 8.17. Амплитудно-фазово-частотная характе­ристика процесса резания

На рис. 8.17 показаны частотные характе­ристики резания применительно к передней и задней поверхностям. Там же показана сум­марная характеристика первого приближения, основанная на допущении, что силы на передней и задней поверхностях действуют по одной пря­мой

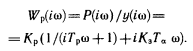
Здесь К_з = Ь₃/Ь, Т_а —постоянная времени заднего угла (формирования сил на задней поверхности резца), с; Т_а = H₃h²₃/(2ʊP_yД} = = l_a /ʊ, где l_a — длина пути резания за вре­мя Т_а.

Характеристика показывает, что в зависи­мости от режимов резания, материала заготов­ки, геометрических параметров и материала режущего инструмента, частоты колебаний сила резания может отставать или опережать по фазе смещение инструмента. При обработке пластич­ных материалов (медь, алюминий, электротех­ническая сталь и т. п.) влияние сил на задней поверхности мало (мало Н₃). При резании твердых или закаленных материалов изменения этих сил играют значительную роль в динами­ческих процессах.

8.2. Коэффициенты динамической характеристики процесса резания

Существенное значение имеет состояние режу­щей кромки (радиус закругления, фаска износа и т. п.). Многообразие условий резания, изменение параметров режущего лезвия по мере его изнашивания определяют соответствующее многообразие значений параметров динами­ческой характеристики резания. Например, при изменении скорости резания стали от 20— 30 м/мин до 100—150 м/мин усадка изменяется в 1,5—2 раза. При изменении радиуса скругления режущей кромки от значения, близкого к нулю, до 1 мм усадка изменяется также в 1,5—2 раза.

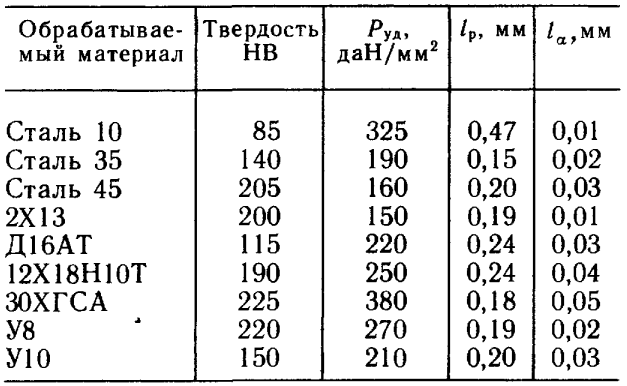
Для расчетов используют значения парамет­ров, типичные для рассматриваемых условий обработки. В табл. 8.2 приведены экспери­ментально полученные средние значения удель­ной силы Р_уд и постоянные пути резания l_р и l_а при обработке различных материалов острозаточенным резцом. Условия обработки: скорость резания 10—160 м/мин; заданная сред­няя толщина срезаемого слоя 0,08 мм; перед­ний угол резца 10°; задний угол 8°; материал резца Т15К6; K₃= 1.

Инструменты цилиндрической формы (шли­фовальные круги, цилиндрические фрезы и т. п.) в процессе обработки срезают слой, имеющий переменное сечение (типа «запятой» и т. п.). Динамическая характеристика реза­ния в этом случае имеет составляющую, определяемую скоростью внедрения, так как врезание изменяет форму срезаемого слоя Соз­дается опережение силы по фазе относитель­но изменения толщины срезаемого слоя.

Устойчивость динамической системы станка при резании оценивается по частотному кри­терию Найквиста. Применение этого крите­рия по отношению к системе с запаздываю­щей связью, возникающей вследствие образо­вания регенеративного эффекта при резании по следу, имеет свою особенность. Она заключа­ется в формировании разомкнутой системы разрывом только связей, включающих элемент запаздывания.

Система устойчива, если характеристика ра­зомкнутой системы (полученная без учета реге­неративного эффекта) лежит справа от некото­рой линии (окружности), семейство которых показано на рис. 8.18. Для предельных зна­чений коэффициента перекрытия получают пря­мую lm₅, параллельную мнимой оси и проходящую через точку «— 0,5» на веществен­ной оси, при коэффициенте перекрытия, рав­ном единице, или точку «—1» на вещественной оси при коэффициенте перекрытия, равном нулю (резание «по чистому»). В последнем случае динамическая система станка устой­чива, если характеристика разомкнутой сис­темы не охватывает точку «—1». На рис. 8.19 показана схема разомкнутой системы при резании «по чистому». Там же показаны ха­рактеристики разомкнутой системы при поло­жительном и отрицательном статическом коэф­фициенте эквивалентной упругой системы: W_Раз(iω)= W_эус(iω)W_p(iω). При этом А_эус(iω) = А_эус(iω)А_р(iω), φ_раз(iω) = φ_эус(iω) + φ_р(iω).

Анализируя возможные модификации харак­теристики разомкнутой системы, можно оценить влияние параметров эквивалентной упругой сис­темы и процесса резания на устойчивость динамической системы станка при резании. Увеличение коэффициента K_Р резания при уве­личении ширины срезаемой стружки ведет к снижению запаса устойчивости. При некотором значении ширины стружки характеристика ра­зомкнутой системы достигает границы, опре­деляемой критерием устойчивости. Такое пре­дельное значение ширины срезаемого слоя по­лучило название «предельной стружки» и явля­ется удобным параметром для оценки качества станка по устойчивости при проектировании и при испытаниях прототипов или серийно вы­пускаемых станков.

Необходимые изменения в конструкции стан­ка, влияющие на повышение устойчивости при резании, оценивают путем анализа формы колебаний на собственной частоте, определяе­мой по той части характеристики разомкнутой системы, которая достигает границы устой­чивости.

После выбора возможных конструктивных решений (повышения жесткости, демпфирова­ния, изменения конфигурации деталей и т. п.) выполняют повторный расчет характеристик. Повторный расчет необходим вследствие значи­тельного влияния связанности колебаний от­дельных форм между собой в сложных колеба­тельных системах. Улучшив характеристику данной формы колебаний, произведенные конструктивные изменения могут сделать по­тенциально неустойчивой другую частотную сос­тавляющую. Это справедливо для всех элемен­тов динамической системы. Например, можно достигнуть увеличения демпфирования колеба­ний токарного станка на низкой частоте, соот­ветствующей интенсивным колебаниям шпин­дельного узла и обрабатываемой заготовки, путем усиления эффекта, оказываемого задней поверхностью резца (создание виброгасящей фаски, расширение зоны контакта вспомога­тельной задней поверхности и т. п.).

В этом случае динамическая характеристика резания показывает увеличение составляющей фазового опережения изменения силы резания по отношению к изменению толщины среза­емого слоя. Однако эта фазовая составляю­щая расширяет высокочастотную составляю­щую характеристики разомкнутой системы и вы­зывает появление интенсивных высокочастотных колебаний инструмента. В таких случаях может быть найдено некоторое компромиссное решение.

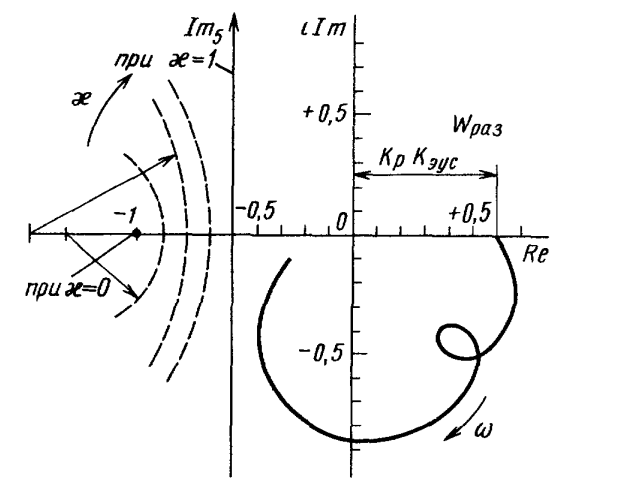
Рис. 8.18. Схема оценки устойчивости динамичес­кой системы станка при резании

Статическая неустойчивость встречается при резании достаточно часто и носит название «подрывание» инструмента Она возникает в тех случаях, когда характеристика разомкну­той системы охватывает точку «—1» на вещест­венной оси при нулевой частоте.

При этом происходит интенсивно нарастаю­щее самопроизвольное врезание инструмента в обрабатываемую заготовку.

Условия потери статической устойчивости или условия подрывания следующие: K_эус<0; K_PK_эус| > 1

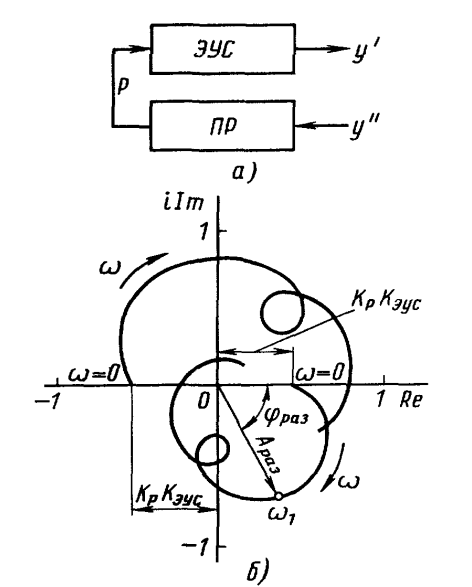
Рис. 8.19. Схема (а) разомкнутой динамической системы станка при резании «по чистому» и ее частот­ные характеристики (б) при положительном и отри­цательном коэффициенте статической характеристи­ки ЭУС

Исключение этих условий достигается путем такой перекомпоновки системы, при которой статическая характеристика эквивалентной упругой системы станет положительной. Воз­можно уменьшение ширины стружки и соот­ветственно коэффициента резания, а также по­вышение жесткости, т. е. уменьшение стати­ческого коэффициента эквивалентной упругой системы.

На токарных станках, особенно на опера­циях отрезания или врезной обработки широ­ким резцом, условия статической потери устой­чивости встречаются часто. Это объясняется спецификой характеристики упругой системы суппортной группы таких станков как одного из случаев реализации статической связи между пространственными деформациями системы.

При формировании элементной стружки или неустойчивого нароста, т. е. при автоколеба­тельном стружкообразовании, сила резания периодически изменяется. В этом случае возни­кает задача оценки колебаний динамической системы станка, вызванных периодически изме­няющейся силой резания. Задача формули­руется как задача взаимодействия автоколе­бательной системы с пассивной колебательной упругой системой. На рис. 8.20 показана схема динамической системы при резании в условиях наростообразования. Связь наростообразования и деформаций упругой системы определяется зависимостью размера нароста от толщины срезаемого слоя, а обратная связь — измене­нием толщины срезаемого слоя, выступающей перед режущей кромкой частью нароста. В ре­зультате анализа такой системы установлена возможность существования двух режимов ко­лебаний, граница между которыми определяет­ся примерным соотношением К_рК_Эус =1.

В случае малой ширины срезаемого слоя и жесткой эквивалентной упругой системы, т. е. при указанном соотношении, меньшем единицы, возникают колебания малой амплиту­ды с частотой «срыва» нароста, возрастающей с ростом скорости резания. Они напоминают обычные вынужденные колебания. При большой ширине срезаемого слоя и малой жесткости, т. е. при соотношении, большем единицы, ин­тенсивность колебаний значительно возрастет, достигая максимума при некоторой скорости резания, а затем убывая. Частота колебаний близка к собственной частоте колебаний упру­гой системы и остается постоянной при измене­нии скорости резания. Нарост срывается с этой же частотой. Скорость резания, при которой амплитуда колебаний максимальна, соответ­ствует условию совпадения частоты естествен­ного формирования нароста с собственной частотой системы.

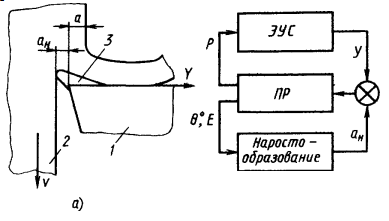
Рис. 8.20. Схема зоны резания (а) и динамической системы станка (б) при резании с неустойчивым наростом:

1— резец; 2— заготовка; 3 — нарост

При проектировании станков следует доби­ваться исключения условий появления автоко­лебаний второго типа.

Реакция устойчивой динамической системы станка при резании на внешние воздействия зависит от вида внешнего воздействия и ха­рактеристики системы. Представляет практичес­кий интерес оценка этой реакции по парамет­ру, определяющему точность обработки. Сле­дует различать воздействия, оказываемые на эквивалентную упругую систему и на процесс резания. Реакция замкнутой системы в ее прос­тейшем эквивалентном виде одноконтурной сис­темы определяется выражениями

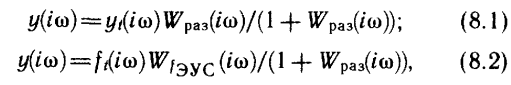
где у(iω) — отклонения заданного положения инструмента перпендикулярно поверхности ре­зания; у_t(iω) = Δ(iω)— заданное изменение тол­щины срезаемого слоя (припуска); f_t(iw) — заданное внешнее воздействие на эквивалент­ную упругую систему; W_fЭУС(iω) — характерис­тика эквивалентной упругой системы по смеще­нию в направлении нормали к поверхности ре­зания при заданном воздействии f(t).

Статическое отклонение при воздействии на процесс резания реализуется при срезании пос­тоянного припуска. Отклонение системы, опре­деляющее статическую погрешность размера заготовки, обрабатываемой на токарном стан­ке, определяется в соответствии с формулой (8.1) при ω=0: у = ɗ = + ΔK_рK_эус/(1 + F K_рK_эус). где ɗ — отклонение радиуса обра­батываемой заготовки; А — заданный постоян­ный припуск (настройка системы).

Знаки погрешности соответствуют плюсу или минусу статической характеристики эквивалент­ной упругой системы. При отрицательной ха­рактеристике размер детали будет меньше заданного. Кроме того, при равенстве нулю знаменателя (что соответствует условию статической неустойчивости — «подрыванию инструмента») отклонение возрастает теорети­чески до бесконечности.

Вынужденные колебания при обработке воз­никают при периодических внешних воздейст­виях. Следует различать внешние воздействия на процесс резания и на эквивалентную упругую систему. Распространена ошибка оцен­ки вынужденных колебаний при периодичес­ком изменении толщины срезаемого слоя, например при фрезеровании как обычных вы­нужденных колебаний упругой системы под действием периодически изменяющейся силы резания. В действительности закономерности этих колебаний иные. Как правило, амплитуды вынужденных колебаний в станках малы, и мож­но ограничиться линейным приближением.

При срезании припуска переменной толщины из выражения (8.1) с учетом правил умно­жения и деления комплексных величин следует: A_у = A_Δ A_раз/A_зн, где A_у — амплитуда колебаний системы (амплитуда следа на поверхности заготовки при резании острым резцом); A_Δ — заданная амплитуда колебаний толщины сре­заемого слоя при заданной частоте; А_раз — амплитуда характеристики разомкнутой систе­мы при заданной частоте колебаний; A_зн — амплитуда частотной характеристики, стоящей в знаменателе выражений (8.1), (8.2), опре­деляющих реакцию системы на внешние воздей­ствия; берут по характеристике разомкнутой системы со смещением начала координат в точку «—1» на вещественной оси (рис. 8.21).

На рис. 8.21 показано построение, необ­ходимое для определения вынужденных колеба­ний при резании. Амплитуда колебаний сис­темы и следа на обработанной поверхности будет меньше заданной амплитуды колебаний толщины срезаемого слоя, если А_раз<А_зн. Для частот воздействия, соответствующих опреде­ленным точкам характеристики разомкнутой системы, это соотношение не превысит единицы при условии расположения точек справа от пря­мой I_ms. Эта прямая ограничивает область устойчивости системы при резании по следу при коэффициенте перекрытия, равном единице.

Особенность такого вида вынужденных колебаний заключается в том, что путем по­вышения динамической жесткости и уменьше­ния ширины срезаемого слоя, т. е. повышения устойчивости системы (уменьшения радиуса- вектора A_раз), можно практически устранить вынужденные колебания, например при фрезе­ровании, даже в случае резания на резо­нансных режимах.

При анализе вынужденных колебаний, выз­ванных воздействием на эквивалентную упругую систему, необходимо расчетным путем или экспе­риментально определить амплитуду колебаний станка при вспомогательных движениях под воздействием f(t) и при соответствующей час­тотной характеристике W_fэус. При неизвестных воздействиях, как показано в подразд. 8.3, оценивают спектр колебаний при вспомогательных движениях. Резание изменяет амплитуды ко­лебаний при вспомогательном ходе: A_f = А_вх(1/A_зн), где A_f — амплитуда вынужден­ных колебаний системы при резании, т. е. волны на обработанной поверхности при реза­нии острым резцом; A_вх—амплитуда вынуж­денных колебаний при вспомогательном ходе на данной частоте воздействия (или спект­ральной составляющей).

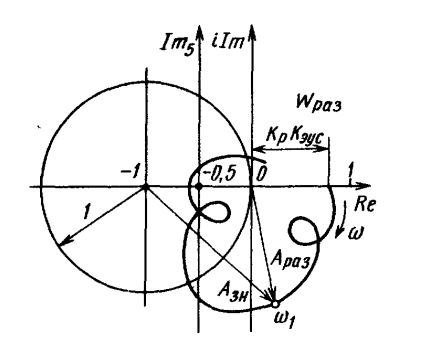
Рис. 8.21. Схема для определения параметров час­тотных характеристик для оценки вынужденных колебаний при внешних воздействиях на процесс резания и на эквивалентную упругую систему

Из приведенного выражения следует, что при резании амплитуды колебаний уменьшаются по сравнению с амплитудами колебаний при вспо­могательном ходе на частотах, соответствую­щих точкам характеристики разомкнутой сис­темы, лежащим за пределами единичной окруж­ности с центром в точке «—1» вещественной оси. На частотах, лежащих внутри окруж­ности, амплитуды колебаний при резании увеличиваются. Если характеристика разомкну­той системы пройдет через точку «—1», то амплитуда на этой частоте возрастет теоре­тически до бесконечности. Это соответствует границе устойчивости системы при резании «по чистому». Особенность этих вынужденных колебаний (на частотах в пределах единичной окружности) заключается в том, что путем повышения устойчивости системы, например уменьшая ширину срезаемого слоя, колебания нельзя устранить. Их можно уменьшить толь­ко до уровня колебаний при вспомогательном ходе.

В связи с этим, как указано в предыдущем подразделе, при проектировании и изготовлении станков необходимо принимать меры по устра­нению или уменьшению колебаний станка при вспомогательном ходе.

Отклонения системы при переходных процес­сах оцениваются главным образом при работе на автоматизированных станках при обработ­ке сложных поверхностей с меняющимся се­чением срезаемого слоя. Во многих случаях отклонения системы таковы, что необходимо учитывать нелинейность характеристик. При решении конкретных задач следует учитывать изложенные в данной главе закономерности, характеризующие особенности динамической системы станка.